La misura della parallasse di un asteroide

Immagine dell'asteroide dedicato all'astronauta italiana Samantha Cristoforetti, ripreso dal nostro Osservatorio (30x15sec).
Lo scorso 3 marzo l’Agenzia Spaziale Europea ha annunciato che Samantha Cristoforetti tornerà in orbita sulla ISS nel 2022. Sarà il suo secondo volo nello spazio dopo la missione Futura del 2014-2015, durante la quale trascorse 199 giorni a bordo della Stazione Spaziale Internazionale.
All’astronauta italiana è dedicato un asteroide della fascia principale tra Marte e Giove, scoperto nel 1998 da Beppe Forti e Maura Tombelli con la camera Schmidt dell’INAF-Osservatorio Astronomico di Asiago.
Nel 2015 l’International Astronomical Union approva la proposta di battezzarlo 15006 Samcristoforetti.
Il 29 marzo 2021 l'INAF ha promosso sul loro sito educational la ripresa da parte degli astrofili dell'asteroide in questione, e noi abbiamo aderito. Tuttavia ho pensato di fare qualcosa in più, e di tentare la misura della sua distanza dalla Terra.
Per farlo, occorre riprenderlo nello stesso istante da due località il più possibile distanti tra loro. Purtroppo l'asteroide (15006) si trova tra Marte e Giove, ed è così distante che non è possibile misurarlo utilizzando due Osservatori in Italia, perchè la base massima (circa 1000 km) è troppo piccola. Occorre utilizzare un Osservatorio molto più distante, e mi è subito venuto in mente lo Skygems Remote Observatory della Namibia, gestito dal collega astrofilo Lukas Demetz.
La sua strumentazione è di prim'ordine, e comprende un bellissimo telescopio da 50cm dall'ottima qualità ottica. Il cielo della Namibia è uno dei migliori al mondo: ottima trasparenza, inquinamento luminoso assente, buon seeing ed un numero elevato di notti serene.

Immagine dell'asteroide ripreso dallo Skygems Remote Observatory della Namibia (3x90sec).
La notte tra il 2 ed il 3 aprile il cielo era sereno da entrambe le località, quindi ho pianificato le riprese, iniziate circa nello stesso momento ma con pose diverse per ogni località (90 secondi di posa dalla Namibia e 15 secondi di posa dal nostro Osservatorio). In questo modo è possibile "giocare" con la somma delle immagini per ottenere un tempo il più possibile simile, idealmente allo stesso secondo.
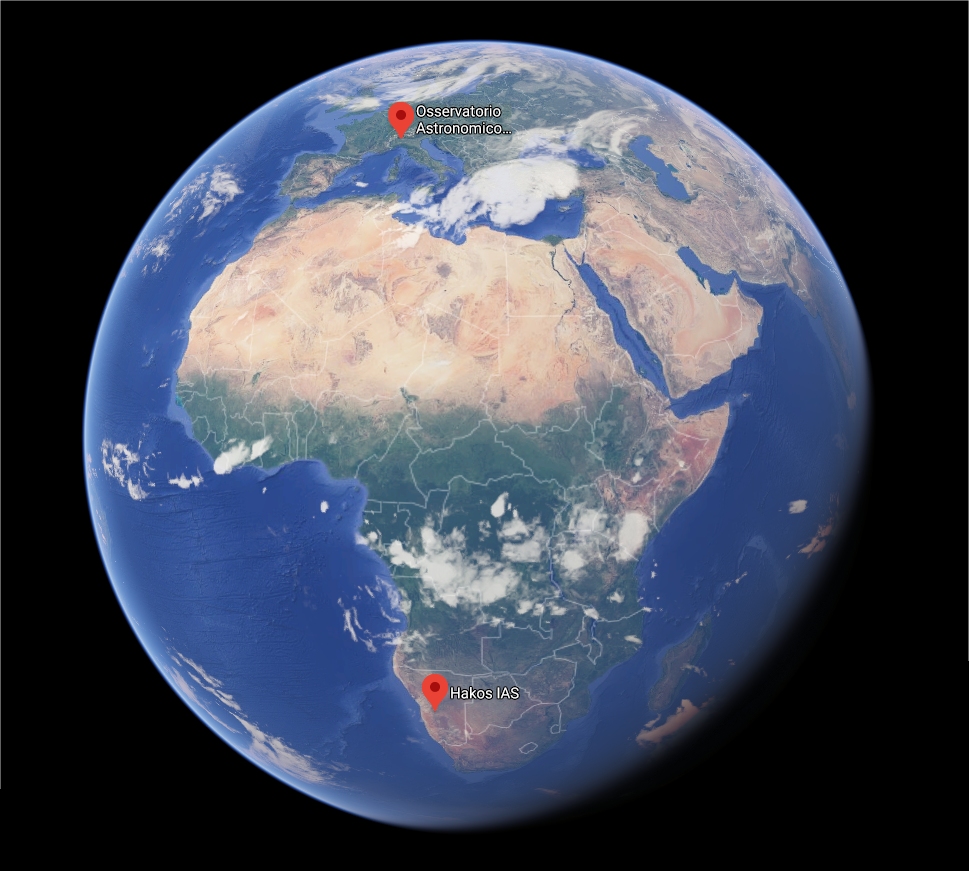
Posizione dei due siti di osservazione.
Utilizzando il software Astrometrica ho sommato le immagini dell'asteroide ottenute in entrambi i siti, come detto selezionando le riprese in maniera da avere il più possibile lo stesso tempo medio, che si è rivelato essere le ore 21:32:09.5 UT (+/- 1 secondo). Di seguito le coordinate celesti:
Osservatorio Schiaparelli (MPC 204):
AR: 11h 50m 01.49s – DEC: +21° 00' 41.4"
Skygems Remote Observatory (MPC L81):
AR: 11h 50m 01.47s – DEC: +21° 00' 45.8"
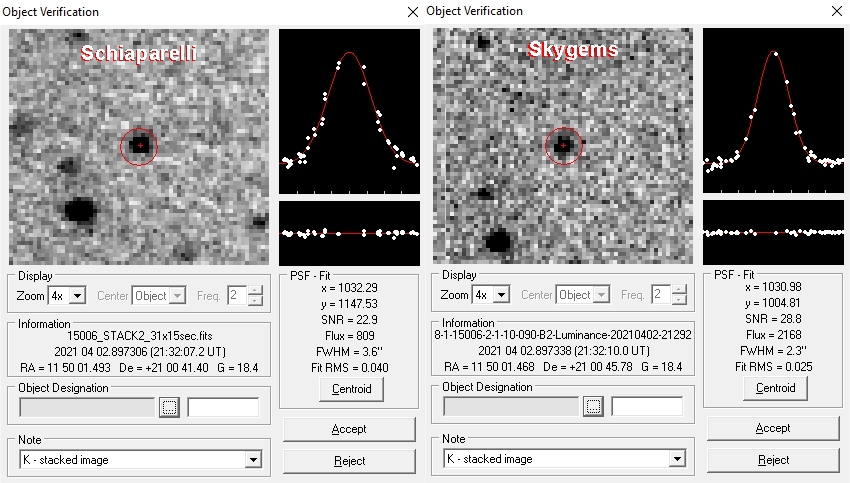
Immagini dell'asteroide riprese dalle due località: si noti come l'asteroide sia leggermente spostato verso l'alto nell'immagine di destra.
La parallasse, ottenuta mediando i valori ottenuti da due serie di immagini diverse, è risultata essere complessivamente 4.34" +/- 0.1", tutta in declinazione vista la preponderante differenza in latitudine dei due siti rispetto alla differenza in longitudine.
Per determinare la distanza angolare tra i due siti si utilizza la seguente formula:
cos (d) = sen (lat1) * sen (lat2) + cos (lat1) * cos (lat2) * cos (dlong)
dove d è l'angolo tra i due Osservatori, lat1 è la latitudine di 204, lat2 è la latitudine di L81 e dlong è la differenza in longitudine dei due siti.
Le coordinate geografiche sono le seguenti:
204 – Schiaparelli
LAT1: 45° 52′ 06” N (45.86778° N) – LONG1: 08° 46′ 12” E (8.77000° E)
L81 – Skygems
LAT2: 23° 14′ 11” S (23.23639° S) – LONG2: 16° 21′ 42” E (16.36167° E)
La formula diventa quindi la seguente:
cos (d) = sen (45.86778) * sen (-23.23639) + cos (45.86778) * cos (-23.23639) * cos (7.59167)
Quindi:
cos (d) = 0.35105
Per determinare d occorre fare l'arcocoseno di questo numero, che equivale a 69,44845 gradi.
Dalla distanza in gradi alla distanza della corda in km si usa la seguente formula:
D = 2 * r * sin (d/2)
dove r è il raggio terrestre (6.371 km).
Il risultato è 7.258 km.
Infine, la distanza dell'asteroide si calcola con la seguente formula:
ASTD = D / tang (p)
dove p è la parallasse in gradi.
Il risultato finale è 344,9 milioni di km, a fronte di una distanza reale di 329,4 milioni di km (fonte NASA Horizons). La differenza è inferiore al 5%, e rientra nell'errore tipico delle misure astrometriche, pari a circa 0.5 secondi d'arco. La parallasse corretta per ottenere il valore di distanza reale è infatti di 4.55".







